
Думаю немного бреда на вторник не сильно повредит рабочей неделе. У меня хобби, на досуге я пытаюсь придумать, как взломать алгоритм майнинга bitcoin, избежать тупого перебора нонсе и находить решение задачи подбора хэша с минимальным расходом энергии. Сразу скажу результата я, конечно, пока не достиг, но тем не менее, почему бы не изложить в письменном виде идеи, которые рождаются в голове? Куда-то же их нужно девать…
Несмотря на бредовость изложенных ниже идей я думаю эта статья может быть полезна тому, кто изучает
- язык C++ и его темплейты
- немного цифровой схемотехники
- немного теории вероятности и вероятностной арифметики
- детально алгоритм хэширования bitcoin
С чего начнем?
Может с последнего и самого скучного пункта этого списка? Потерпите, дальше будет веселее.
Рассмотрим детально алгоритм вычисления хэширующей функции bitcoin. Она простая F(x)=sha256(sha256(x)), где x — это входные данные 80 байт, заголовок блока вместе с номером версии блока, prev block hash, merkle root, timestamp, bits и nonce. Вот примеры довольно свежих заголовков блоков, которые передаются хэширующей функции:
//blk=533522
0x00,0x00,0x00,0x20,
0x6d,0xa5,0xdd,0xb5,0x78,0x04,0x08,0x80,0xae,0x3d,0xed,0xc5,0x8e,0xe9,0x74,0x93,0x93,0x6d,0x6a,0xf4,0x0e,0x80,0x30,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0xdf,0x3e,0xb0,0xf4,0x92,0xbf,0xe9,0xb8,0xc8,0x12,0x1f,0x84,0xdd,0x35,0xe1,0x38,0x09,0xcc,0x28,0xc2,0x33,0x53,0x90,0x4e,0x15,0x49,0x5e,0xc7,0xb0,0x78,0x35,0x91,
0x82,0xDB,0x57,0x5B,
0x17,0x5A,0x36,0x17,
0xAA,0x02,0x44,0x22,
//blk=533523
0x00,0x00,0x00,0x20,
0x6a,0x27,0x37,0xc3,0x1f,0x68,0xf8,0xe3,0x03,0xa3,0x5d,0xff,0x2d,0x97,0x39,0xaf,0x81,0xa2,0xf5,0xf0,0x7c,0xdb,0x34,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0xa1,0xb8,0x4f,0x75,0x66,0xf3,0xf3,0x8e,0x78,0xf7,0xa2,0xa2,0xa2,0x19,0xa1,0x18,0x45,0xfa,0x58,0x53,0xe4,0x05,0x50,0x12,0x57,0xa1,0xab,0x2c,0x39,0xe6,0x1f,0x63,
0xA0,0xDB,0x57,0x5B,
0x17,0x5A,0x36,0x17,
0x84,0x7B,0x86,0xE7,
//blk=533524
0x00,0x00,0x00,0x20,
0xb3,0xc7,0xaa,0x07,0x26,0xdb,0xe8,0x58,0x19,0xa8,0xb9,0x53,0x08,0x62,0x8b,0xca,0x58,0x00,0x69,0x64,0x58,0x69,0x1a,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x4e,0xfc,0xf4,0x5c,0xad,0x31,0x44,0x5b,0xb1,0x13,0x80,0x03,0xe0,0xfd,0x04,0x24,0x86,0xcc,0x7a,0x8c,0xa7,0x7c,0x30,0x60,0x05,0x6f,0x43,0xcf,0x25,0x45,0x8f,0xd8,
0x80,0xDE,0x57,0x5B,
0x17,0x5A,0x36,0x17,
0xF7,0x2B,0x3B,0x42,
Этот набор байтов довольно ценный материал, так как зачастую по исходникам майнеров не просто понять в каком порядке должны следовать байты при формировании заголовка, часто применяется разворот местами младших и старших байт (endians).
Итак, от заголовка блока, 80 байт считается хэш sha256 и потом от результата еще sha256.
Сам по себе алгоритм sha256, если посмотреть в разных источниках обычно состоит из четырех функций:
- void sha256_init(SHA256_CTX *ctx);
- void sha256_transform(SHA256_CTX *ctx, const BYTE data[]);
- void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len);
- void sha256_final(SHA256_CTX *ctx, BYTE hash[]);
Первая функция, которая вызывается при расчете хэша — это sha256_init(), приводит в исходное состояние структуру SHA256_CTX. Там так то особо ничего нет важного кроме восьми 32х битных слова state, которые изначально заполняются специальными словами:
void sha256_init(SHA256_CTX *ctx){
ctx->datalen = 0;
ctx->bitlen = 0;
ctx->state[0] = 0x6a09e667;
ctx->state[1] = 0xbb67ae85;
ctx->state[2] = 0x3c6ef372;
ctx->state[3] = 0xa54ff53a;
ctx->state[4] = 0x510e527f;
ctx->state[5] = 0x9b05688c;
ctx->state[6] = 0x1f83d9ab;
ctx->state[7] = 0x5be0cd19;
}
Предположим у нас есть файл, хэш которого нужно посчитать. Читаем файл блоками произвольного размера и вызываем функцию sha256_update() куда передаем указатель на данные блока и длину блока. Функция накапливает хэш в структуре SHA256_CTX в массиве state:
void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len){
uint32_t i;
for (i = 0; i < len; ++i) {
ctx->data[ctx->datalen] = data[i];
ctx->datalen++;
if (ctx->datalen == 64) {
sha256_transform(ctx, ctx->data);
ctx->bitlen += 512;
ctx->datalen = 0;
}
}
}
Сама по себе sha256_update() вызывает функцию рабочую лошадку sha256_transform(), которая принимает уже блоки только фиксированной длины по 64 байта:
/****************************** MACROS ******************************/
#define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b))))
#define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b))))
#define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z)))
#define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z)))
#define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22))
#define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25))
#define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3))
#define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10))
/**************************** VARIABLES *****************************/
static const uint32_t k[64] = {
0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5,
0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174,
0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da,
0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967,
0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85,
0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070,
0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3,
0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2
};
/*********************** FUNCTION DEFINITIONS ***********************/
void sha256_transform(SHA256_CTX *ctx, const BYTE data[]){
uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64];
for (i = 0, j = 0; i < 16; ++i, j += 4)
m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]);
for (; i < 64; ++i)
m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16];
a = ctx->state[0];
b = ctx->state[1];
c = ctx->state[2];
d = ctx->state[3];
e = ctx->state[4];
f = ctx->state[5];
g = ctx->state[6];
h = ctx->state[7];
for (i = 0; i < 64; ++i) {
t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i];
t2 = EP0(a) + MAJ(a, b, c);
h = g;
g = f;
f = e;
e = d + t1;
d = c;
c = b;
b = a;
a = t1 + t2;
}
ctx->state[0] += a;
ctx->state[1] += b;
ctx->state[2] += c;
ctx->state[3] += d;
ctx->state[4] += e;
ctx->state[5] += f;
ctx->state[6] += g;
ctx->state[7] += h;
}
Когда хэшируемый файл весь считан и уже передан в функцию sha256_update() остается только вызвать завершающую функцию sha256_final(), которая если размер файла был не кратен 64 байтам, то добавит дополнительные padding байты, впишет в конец последнего блока данных общую длину данных в битах и сделает финальный sha256_transform().
Результат хэширования остается в массиве state.
Это так сказать «высокий уровень».
Применительно к майнеру биткоина, конечно разработчики думают как бы считать поменьше да поэффективней.
Все просто: заголовок содержит всего 80 байт, что не кратно 64 байтам. Таким образом нужно было бы для первого sha256 уже делать два sha256_transform(). Однако по счастью для майнеров, nonce блока находится в конце заголовка, значит первый sha256_transform() можно выполнить всего один раз — это будет так называемый midstate. Далее майнер перебирает все варианты нонсе, которых 4 миллиарда, 2^32 и подставляет их в соответствующее поле для второго sha256_transform(). Этот трансформ завершает первую функцию sha256. Ее результат — это восемь 32х битных слов, то есть 32 байта. От них найти sha256 просто — вызывается завершающий sha256_transform() и все — готово. Заметьте, что входные данные 32 байта меньше по размеру, чем нужные для sha256_transform() 64 байта. Значит опять блок будет дополнен нулями и в конец будет вписана длина блока.
Итого всего три вызова sha256_transform() из которых первый нужно считать только один раз для вычисления midstate.
Я попытался развернуть все манипуляции с данными происходящие при вычислении хэша заголовка блока биткоина в единую функцию, так, чтобы было понятно, как происходит все вычисление конкретно для биткоина и вот что получилось:
//get bitcoin header via ptr to 80 bytes and calc hash
template <typename T>
void full_btc_hash(const uint8_t* ptr80, T nonce, T* presult){
//-1------------------------------------------
//init sha256 state s[7:0]
T s[16];
for (int i = 0; i < 8; i++) {
s[i] = sha256_init_state[i];
presult[i] = sha256_init_state[i];
}
uint8_t tail2[] = {
0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x01,0x00,
};
uint32_t* p = (uint32_t*)tail2;
for (int i = 0; i < 8; i++) {
s[i + 8] = ntohl(p[i]);
}
//get first block for sha256
uint8_t tail[] = { /* 2nd sha256 block padding */
0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x02,0x80
};
T blk1[32];
p = (uint32_t*)ptr80;
for (int i = 0; i < 19; i++) {
blk1[i] = ntohl(p[i]);
}
//put nonce here
blk1[19] = nonce;
p = (uint32_t*)tail;
for (int i = 0; i < 12; i++) {
blk1[i + 20] = ntohl(p[i]);
}
sha256_transform(s, &blk1[0]); //warning! this can be called only once and produce MIDSTATE
sha256_transform(s, &blk1[16]);
sha256_transform(presult, s);
}
Я реализовал эту функцию как c++ template, она у меня может оперировать не просто 32х битными словами скажем uint32_t, но точно так же оперировать словами иного типа «T». У меня здесь и состояние sha256 хранится в виде массива типа «T» и sha256_transform() вызывается с параметром указателем на массив типа «T» и результат возвращается такой же. Трансформ функция теперь тоже в виде c++ template:
template <typename T>
T ror32(T word, unsignedint shift){
return (word >> shift) | (word << (32 - shift));
}
template <typename T>
T Ch(T x, T y, T z){
return z ^ (x & (y ^ z));
}
template<typename T>
T Maj(T x, T y, T z){
return (x & y) | (z & (x | y));
}
#define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22))
#define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25))
#define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3))
#define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10))
unsigned int ntohl(unsignedint in){
return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24);
}
template <typename T>
void LOAD_OP(int I, T *W, const u8 *input){
//W[I] = /*ntohl*/ (((u32*)(input))[I]);
W[I] = ntohl(((u32*)(input))[I]);
//W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]);
}
template <typename T>
void BLEND_OP(int I, T *W){
W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16];
}
template <typename T>
void sha256_transform(T *state, const T *input){
T a, b, c, d, e, f, g, h, t1, t2;
T W[64];
int i;
/* load the input */
for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes
W[i] = input[i];
/* now blend */
for (i = 16; i < 64; i++)
BLEND_OP(i, W);
/* load the state into our registers */
a = state[0]; b = state[1]; c = state[2]; d = state[3];
e = state[4]; f = state[5]; g = state[6]; h = state[7];
//
t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56];
t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2;
t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57];
t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2;
t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58];
t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2;
t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59];
t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2;
t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60];
t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2;
t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61];
t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2;
t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62];
t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2;
t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63];
t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2;
state[0] += a; state[1] += b; state[2] += c; state[3] += d;
state[4] += e; state[5] += f; state[6] += g; state[7] += h;
}
Использование C++ template функций удобно тем, что я могу вычислить нужный мне хэш от обычных данных и получить обычный результат:
const uint8_t header[] = {
0x02,0x00,0x00,0x00,
0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7,
0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55,
0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17,
0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1,
0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44,
0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a,
0x19,0xc8,0xe6,0xba,
0xdc,0x14,0x17,0x87,
0x35,0x8b,0x05,0x53,
0x53,0x5f,0x01,0x19,
0x48,0x75,0x08,0x33
};
uint32_t test_nonce = 0x48750833;
uint32_t result[8];
full_btc_hash(header, test_nonce, result);
uint8_t* presult = (uint8_t * )result;
for (int i = 0; i < 32; i++)
printf("%02X ", presult[i]);
Получается:
92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00
В конце хэша много нулей, красивый хэш, бинго и т.д.
А теперь дальше я могу передать в эту хэширующую функцию не обычные uint32_t данные, а мой специальный C++ класс, который переопределит всю арифметику.
Да-да. Я собираюсь применить «альтернативную» вероятностную математику.
Сам придумал, сам реализовал, сам испытал. Похоже не очень работает. Шутка. Должно работать. Возможно даже не я первый такое пытаюсь провернуть.
Теперь переходим к самому интересному.
Вся арифметика в цифровой электронике выполняется, как операции над битами, и она строго определена операциями И, ИЛИ, НЕ, ИСКЛЮЧАЮЩЕЕ ИЛИ. Ну мы все знаем, что такое таблицы истинности в булевой алгебре.
Я предлагаю добавить немного неопределенности в вычисления, сделать их вероятностными.
Пусть у каждого бита в слове будут не только возможные значения НОЛЬ и ЕДИНИЦА, но и все промежуточные! Я предлагаю рассматривать значение бита, как вероятность события, которое может произойти, а может не произойти. Если все исходные данные достоверно известны, то получается достоверным и результат. А если некоторых данных немного не хватает, то и результат получится с некоторой вероятностью.
В самом деле, предположим, есть два независимых события «a» и «b», вероятности выпадения которых естественно от нуля до единицы соответственно Pa и Pb. Какова вероятность того, что события случатся одновременно? Я уверен, что каждый из нас без колебаний ответит P = Pa * Pb и это правильный ответ!
3D график такой функции будет выглядеть вот так (с двух разных точек зрения):
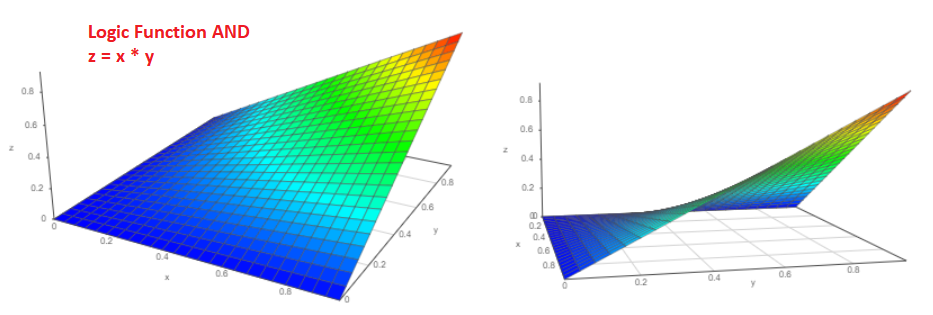
А какова вероятность того, что случится или событие Pa или событие Pb?
Вероятность P = Pa+Pb-Pa*Pb. График функции вот такой:
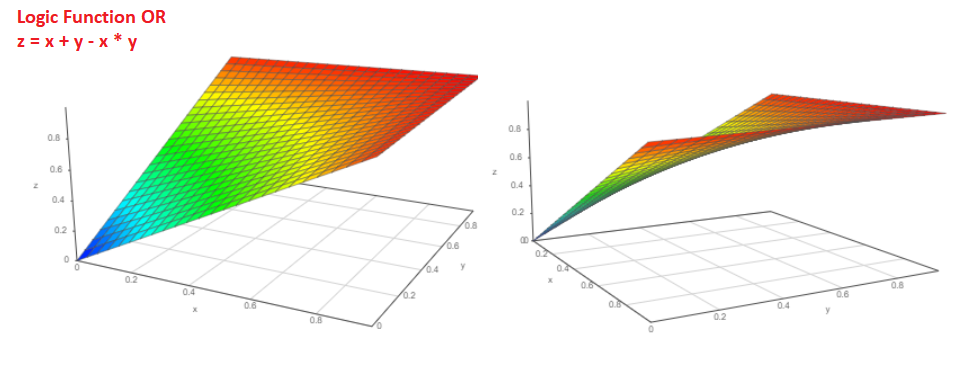
А если мы знаем вероятность выпадения события Pa, то какова вероятность, что событие не произойдет?
P = 1 — Pa.
Теперь сделаем допущение. Представьте себе, что у нас появились логические элементы, которые вычисляют вероятность выходного события, зная вероятность входных событий:
Имея такие логические элементы можно без труда сделать из них более сложные, например, исключающее или, XOR:
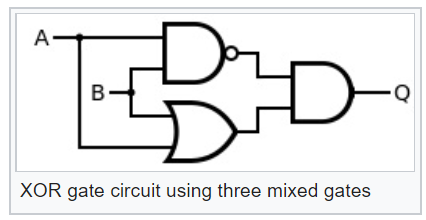
Теперь глядя на схему этого логического элемента XOR, можно понять какова будет вероятность события на выходе вероятностного XOR:
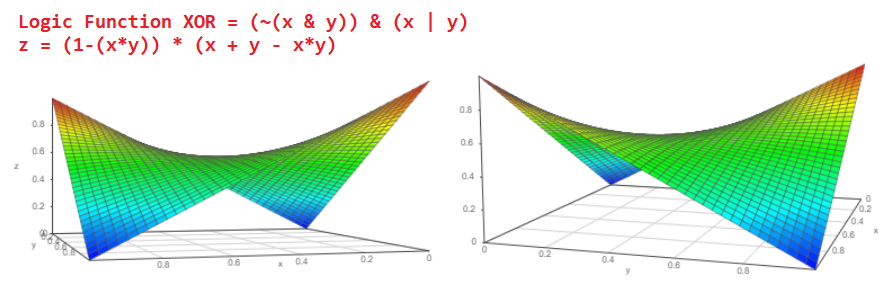
Но и это не все. Мы знаем типовую логическую схему полного сумматора и изнаем, как из полного сумматора делается многоразрядный сумматор:
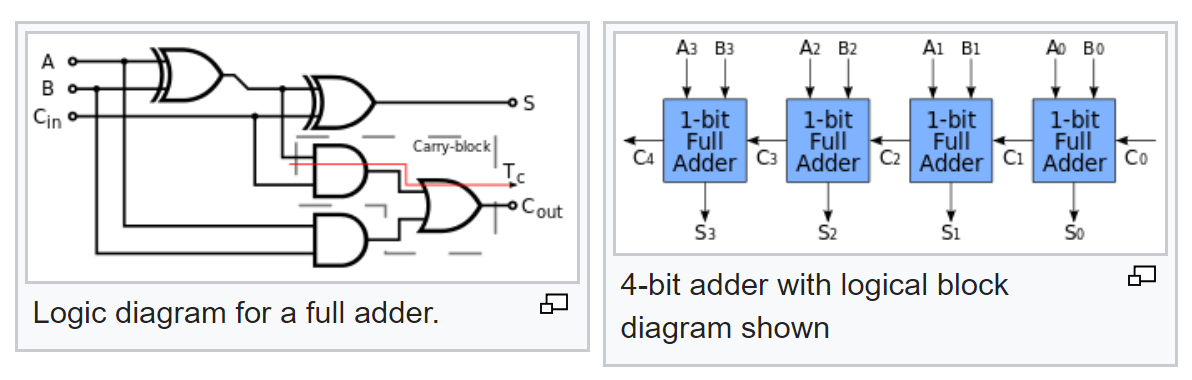
Значит теперь по его схеме теперь мы можем вычислить вероятности сигналов на его выходе, при известных вероятностях сигналов на входе.
Таким образом, я могу реализовать на c++ свой собственный «32х битный» класс (назову его x32) c вероятностной арифметикой, переопределить у этого класса все нужные для sha256 операции вроде AND, OR, XOR, ADD и сдвигов. Класс будет хранить внутри 32 бита, но каждый бит в виде числа с плавающей точкой. Каждая логическая или арифметическая операция над таким 32х битным числом будет вычислять вероятность значения каждого бита при известных или малоизвестных входных параметрах логической или арифметической операции.
Рассмотрим такой очень простой пример, который использует мою вероятностную математику:
typedef std::numeric_limits< double > dbl;
int main(int argc, char *argv[]){
cout.precision(dbl::max_digits10);
x32 a = 0xaabbccdd;
x32 b = 0x12345678;
<b>//b.setBit( 4, 0.75 );</b>
x32 c = a + b;
cout << std::hex << "result = 0x" << c.get32() << "\n" << std::dec;
for (int i = 0; i < 32; i++)
cout << "bit" << i << " = " << c.get_bvi(i) << "\n";
cout << "ok\n";
}
В этом примере суммируются два 32х битных числа.
Пока строка b.setBit( 4, 0.75 ); закомментирована результат сложения точно предсказуем и предопределен, ведь все входные данные для сложения известны. Программа напечатает в консоль вот такое:
result = 0xbcf02355
bit0 = 1
bit1 = 0
bit2 = 1
bit3 = 0
bit4 = 1
bit5 = 0
bit6 = 1
bit7 = 0
bit8 = 1
bit9 = 1
bit10 = 0
bit11 = 0
bit12 = 0
bit13 = 1
bit14 = 0
bit15 = 0
bit16 = 0
bit17 = 0
bit18 = 0
bit19 = 0
bit20 = 1
bit21 = 1
bit22 = 1
bit23 = 1
bit24 = 0
bit25 = 0
bit26 = 1
bit27 = 1
bit28 = 1
bit29 = 1
bit30 = 0
bit31 = 1
Если же раскомментировать строку b.setBit( 4, 0.75 );, то этим самым я как бы говорю программе: «сложи мне эти два числа, только я не очень знаю значение бита 4 второго аргумента, думаю с вероятностью 0.75 это единица».
Тогда сложение происходит, как ему и положено, с полным вычислением вероятностей выходных сигналов, то есть битов:
bit not stable
bit not stable
bit not stable
result = 0xbcf02305
bit0 = 1
bit1 = 0
bit2 = 1
bit3 = 0
bit4 = 0.75
bit5 = 0.1875
bit6 = 0.8125
bit7 = 0
bit8 = 1
bit9 = 1
bit10 = 0
bit11 = 0
bit12 = 0
bit13 = 1
bit14 = 0
bit15 = 0
bit16 = 0
bit17 = 0
bit18 = 0
bit19 = 0
bit20 = 1
bit21 = 1
bit22 = 1
bit23 = 1
bit24 = 0
bit25 = 0
bit26 = 1
bit27 = 1
bit28 = 1
bit29 = 1
bit30 = 0
bit31 = 1
Из-за того, что входные данные были не очень известны получается не очень известным и результат. При этом то, что можно достоверно посчитать считается достоверно. Что нельзя посчитать считается с вероятностью.
Теперь, когда у меня есть такой замечательный 32х битный c++ класс для нечеткой арифметики, я смогу передавать в template функцию full_btc_hash() массивы переменных типа x32 и получать вероятностный оценочный результат хэша.
Для чего все это нужно?
Майнер биткоин заранее не знает, какое нужно выбрать значение 32х битного nonce. Майнер вынужден перебирать их все 4 миллиарда, чтобы считать хэш, пока он не станет «красивым», пока значение хэша не станет меньше target.
Нечеткая вероятностная арифметика теоретически позволяет избавится от перебора.
Да, я изначально не знаю значения всех нужных битов нонсе. Если я их не знаю, что пусть будет ни-то ни-сё — начальная вероятность нонсе битов 0.5. Даже при таком раскладе я могу посчитать вероятность выходных битов хэша. Где-то что-то они получаются так же около 0.5 плюс-минус пол копейки.
Однако, теперь я могу изменить только один бит нонсе с 0.5 до 0.9 или до 0.1 или до 1.0 и посмотреть, как изменится значение вероятности значения сигнала каждого бита хэш функции на выходе. Теперь у меня гораздо больше оценочной информации. Я теперь могу пощупать каждый входной бит нонсе в отдельности и посмотреть куда сдвигается вероятность сигнала на каждом из выходных битов хэш функции.
Например, вот фрагмент, который считает хэш функцию при полностью неизвестных битах нонсе, когда вероятность значения его бит равна 0.5 и второе вычисление, когда предполагаем, что значение бита nonce[0] = 0.9:
typedef std::numeric_limits< double > dbl;
int main(int argc, char *argv[]){
cout.precision(dbl::max_digits10);
//---------------------------------
//hash: 502A989242BDFA912DA58A972836C9CDFEDD4A0278A467E00000000000000000
const u8 strxx[] = {
0x02,0x00,0x00,0x00,
0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7,
0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55,
0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17,
0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00,
0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1,
0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44,
0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a,
0x19,0xc8,0xe6,0xba,
0xdc,0x14,0x17,0x87,
0x35,0x8b,0x05,0x53,
0x53,0x5f,0x01,0x19,
0x48,0x75,0x08,0x33
};
double nonce_bits[32];
for (int i = 0; i < 32; i++)
nonce_bits[i] = 0.5;
x32 nonce_x32_a;
x32 nonce_x32_b;
nonce_x32_a.init(nonce_bits);
nonce_bits[0] = 0.9;
nonce_x32_b.init(nonce_bits);
x32 result_x32_a[8];
x32 result_x32_b[8];
full_btc_hash(strxx, nonce_x32_a, result_x32_a);
full_btc_hash(strxx, nonce_x32_b, result_x32_b);
for (int i = 0; i < 32; i++)
cout << result_x32_a[7].get_bvi(i) << " " << result_x32_b[7].get_bvi(i) << "\n";
Функция класса x32::get_bvi() возвращает вероятность значения бита этого числа.
Вычисляем и видим, что если изменить значение бита nonce[0] с 0.5 до 0.9, то некоторые биты выходного хэша еле качнулись вверх, а некоторые еле качнулись вниз:
0.44525679540883948 0.44525679540840074
0.55268174813167364 0.5526817481315932
0.57758654725359399 0.57758654725360606
0.49595026978928474 0.49595026978930477
0.57118578561406703 0.57118578561407746
0.53237003739057907 0.5323700373905661
0.57269859374138096 0.57269859374138162
0.57631236396381141 0.5763123639638157
0.47943176373960149 0.47943176373960219
0.54955992675177704 0.5495599267517755
0.53321116270879686 0.53321116270879733
0.57294025883744952 0.57294025883744984
0.53131857821387693 0.53131857821387655
0.57253530821899101 0.57253530821899102
0.50661432403287194 0.50661432403287198
0.57149419848354913 0.57149419848354916
0.53220327148366491 0.53220327148366487
0.57268927270412251 0.57268927270412251
0.57632130426913003 0.57632130426913005
0.57233970084776142 0.57233970084776143
0.56824728628552812 0.56824728628552813
0.45247155441889921 0.45247155441889922
0.56875940568326509 0.56875940568326509
0.57524323439326321 0.57524323439326321
0.57587726902392535 0.57587726902392535
0.57597043124557292 0.57597043124557292
0.52847748894672118 0.52847748894672118
0.54512141953055808 0.54512141953055808
0.57362254577539695 0.57362254577539695
0.53082194129771177 0.53082194129771177
0.54404489702929382 0.54404489702929382
0.54065386336136847 0.54065386336136847
Эдакое дыхание ветерка, еле заметное изменение вероятностей на выходе в 10м знаке после запятой. Ну тем не менее… на этом можно пытаться строить какие-то предположения. Красиво выходит, правда?
Кстати, если входные биты входного нонсе проинициализировать правильными, нужными значениями вероятности, типа вот так:
double nonce_bits[32];
for (int i = 0; i < 32; i++)
nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0;
x32 nonce_x32;
nonce_x32.init(nonce_bits);
full_btc_hash(strxx, nonce_x32, result_x32);
то вычисляя вероятностный хэш получаем закономерный правильный результат — «красивый» хэш на выходе, бинго.
Так что с математикой тут все правильно.
Осталось научиться анализировать дыхание ветерка… и хэш сломан.
Звучит, как бред, но это и есть бред — а я в самом начале предупреждал.


